It's all about the Lasso!
We ropin' wild horses?
No, the lasso is another regression function. Linear regression is the one we are most familiar with. This is simply a line that best fits the data. Remember, the data can have as many dimensions as you like. There will still be a line that best fits the data, even if this is impossible to truly visualize beyond 3 dimensions (at least for me!) The line will be more influenced by dimensions that affect the outcome more. This can be seen by looking at the beta coefficient.
Do you remember the ridge regression that we used earlier? This is similar to a regression except that it shrinks each coefficient based on a user supplied hyperparameter using a penalty term. The penalty term introduces a "bias" meaning that it is on average now not "correct." However, increasing the bias can decrease the variance meaning that overall prediction accuracy can be improved.
Let's dip into this a little more, but let's back it up again all the way to a linear regression. Here is a linear regression that is using the sensor signals to predict "power" and then comparing it to the power calculated by the sensor.
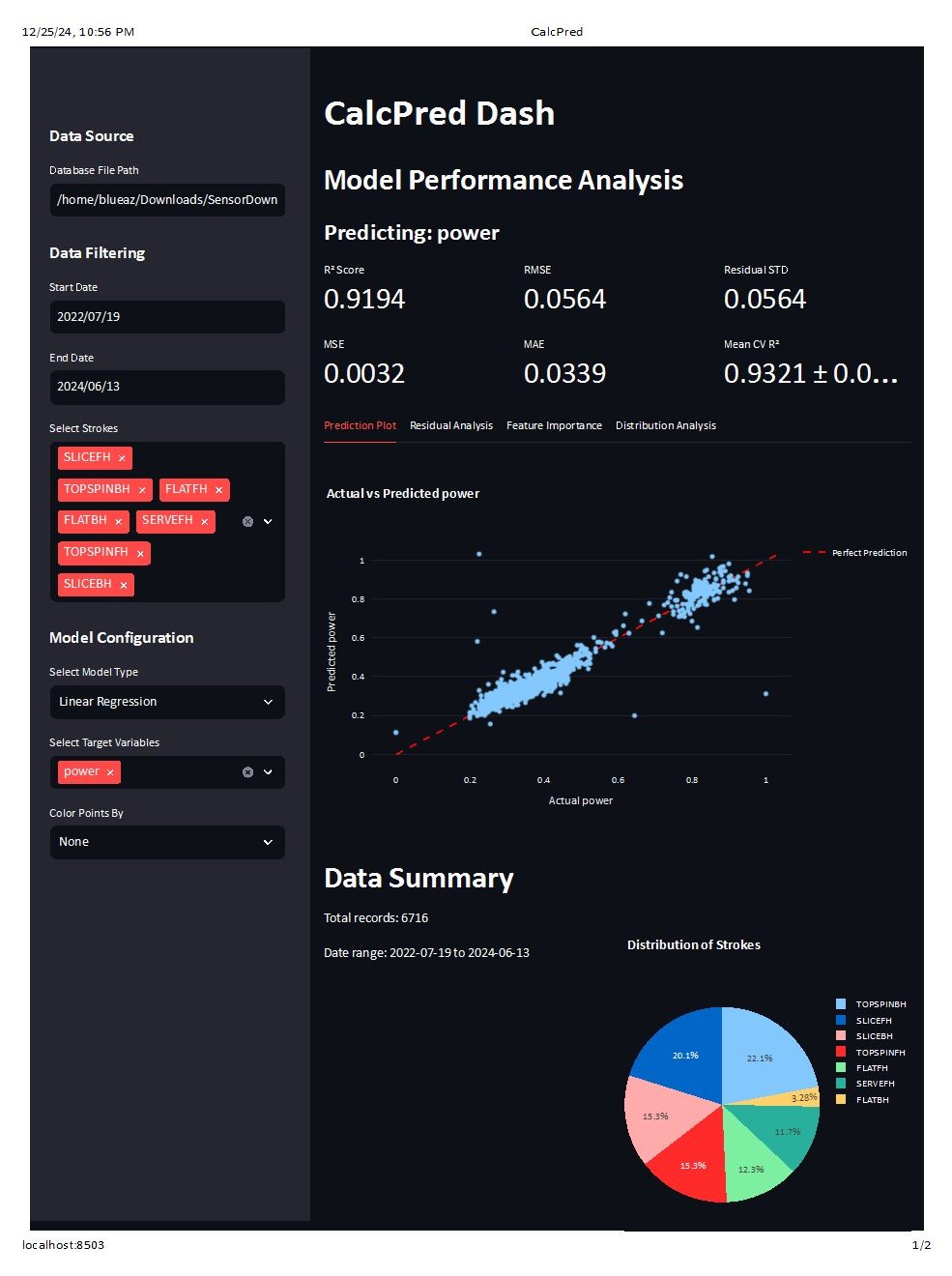
Here we get a full regression report that shows we have a very good fit (>.9) and our input factors largely explain our output. This also shows that the sensor uses something different that a linear regression, but also that it's using something that is pretty close to a linear regression.
Now let's look more closely at how much each of the factors influence the regression. We can do this by looking at the feature importances:
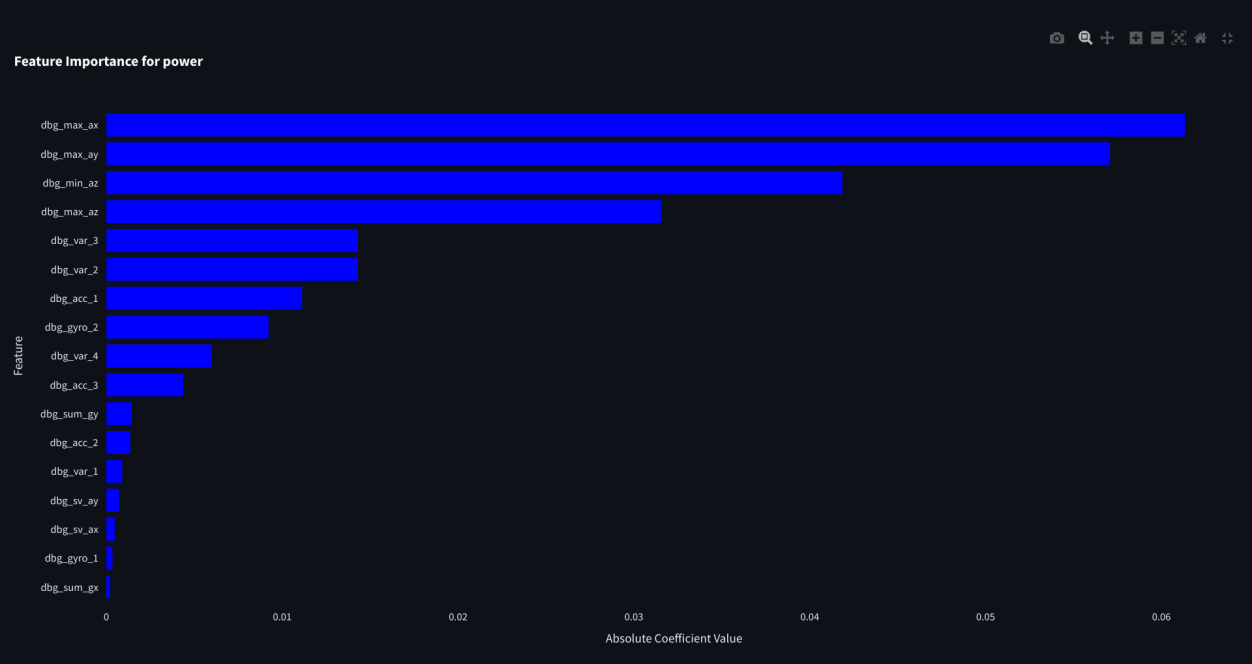
I thought we were talking about ridge?

We're getting there...
Let's look at the same report as before, but this time as a ridge. You might notice that the R^2 is exactly the same as the linear regression. Does this mean there is no difference?
Here we get a full regression report that shows we have a very good fit (>.9) and our input factors largely explain our output. This also shows that the sensor uses something different that a linear regression, but also that it's using something that is pretty close to a linear regression.
Now let's look more closely at how much each of the factors influence the regression. We can do this by looking at the feature importances:


We're getting there...
Let's look at the same report as before, but this time as a ridge. You might notice that the R^2 is exactly the same as the linear regression. Does this mean there is no difference?
No difference?
That's because we are using a regularization factor of 0. This means that each beta isn't penalized and it is acting as a typical linear regression.
Let's see what happens when we increase the alpha:
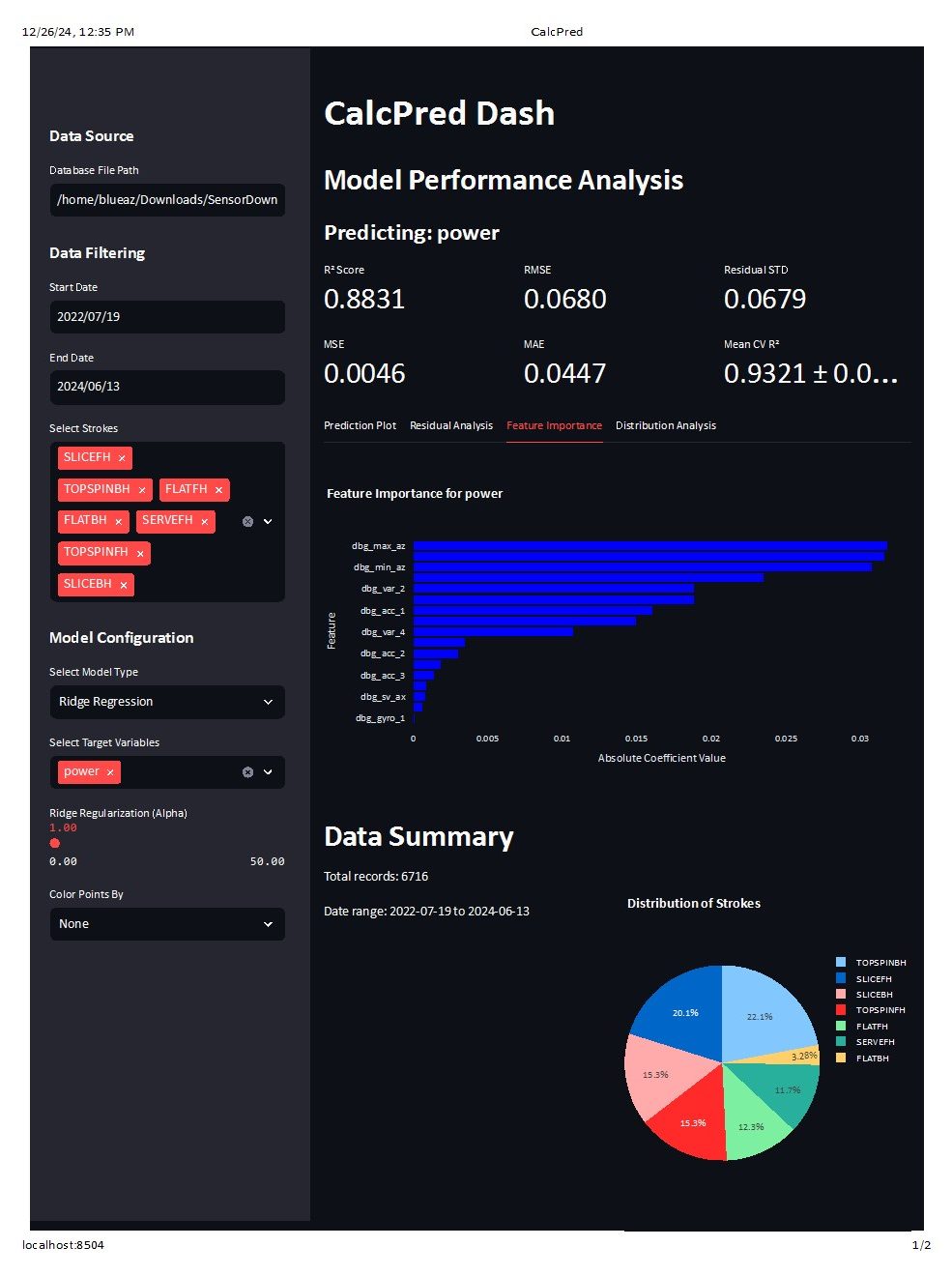
You might notice a few things here. First, the features look like they have the same shape, but the R^2 has dropped to .88. You'll have to believe me also that the feature importance coefficients have shrunk.
Is this a worse model? Well, no, not necessarily. But it does have a lower R^2 because it is biased. It predicts less of the training data because it ignores some information.
But, this could be good! Our overall goal is MSE reduction, so this model might be able to give us reduced variance.
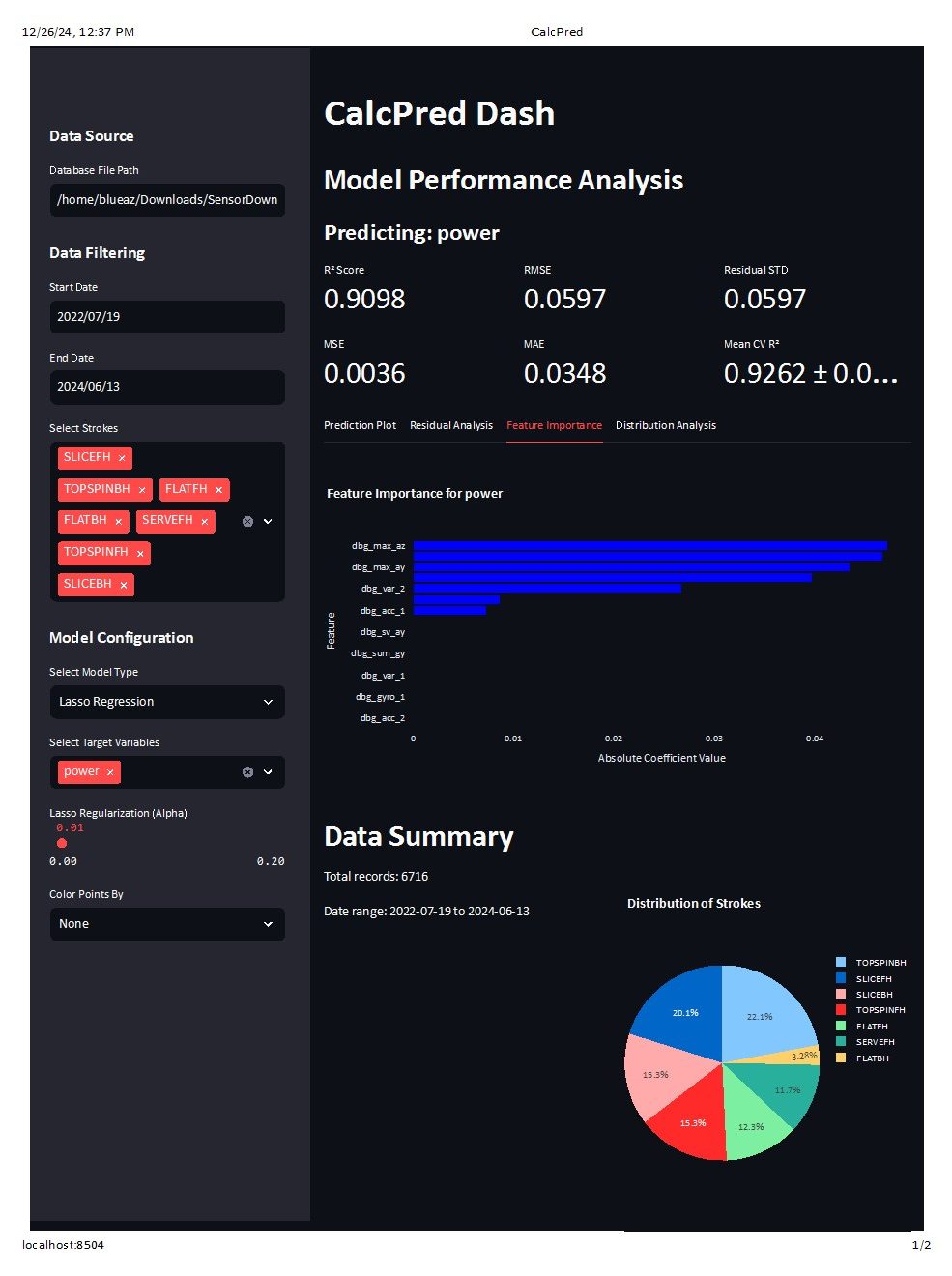
Ok, but we were really here to talk about the lasso. The lasso is almost exactly the same, but instead of driving all of the factors down, it drives down the weaker factors to zero before entirely removing them from the model.
Let's see it in action:
See how the model has dropped to around .9 R^2. We are seeing the same phenomenon as with the ridge. The estimate is now biased.
But, it's getting there in a different way than the ridge. The main factors still have the same coefficients, but the weaker factors are now dropped from the model.
Which is better?
Well, like most things in life, that really depends on what the purpose behind what the models are being used for.
Done?
We certainly could be!
This is some pretty extensive analysis!
But, there's always room for more...
The forehand slice is one shot that I really think needs more analysis. Or, maybe less. As I've mentioned before, the forehand slices is a very unusual shot. It basically is never hit on purpose other than to start a rally or in defensive situations. This sensor is known to have been only used in practice, so I'm surprised so many forehand slices are registered. Have a look at the shot distribution:
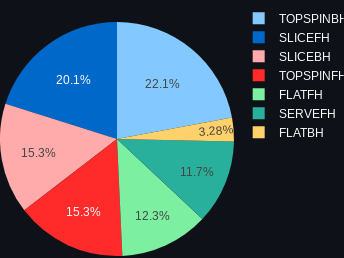
Slice forehand is the 2nd highest registered shot. Even considering the setup shots (remember the "lobe" from the previous analysis?) I really believe that something strange is going on with this shot.
The residual distribution plot also shows a bimodal distribution, which as we learned previously, is usually not desired.
Let's try removing forehand slices from the model and see what happens:
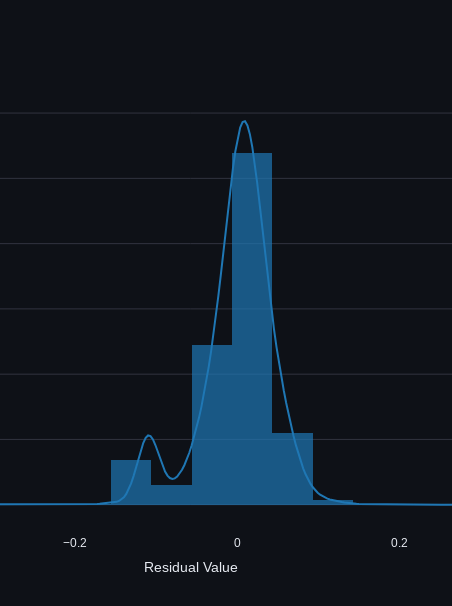
Sure enough! The R^2 has jumped to .94 and we don't have a bimodality in our data. I think this is a good sign that our model is getting stronger when we remove the weakest data from the dataset.
Takeaway?
Again, this seems to be the big problem with tennis sensors. It's really hard to know what to make of anything.
It's certainly useful to track matches using the POP and the Zepp provides some amount of real-time feedback. The Zepp2 (*sad trombone*) was the best of both worlds in that it could track matches and also provide real time practice feedback.
The real future probably lies in the iPhone recording apps, although this comes with some drawbacks of its own. Tennis seems to be progressing quickly so there's a chance that there will be "smart" courts, which will provide the most interesting feedback (whether a ball is in or out) but it's hard to believe that this will be anytime soon.
We need your consent to load the translations
We use a third-party service to translate the website content that may collect data about your activity. Please review the details in the privacy policy and accept the service to view the translations.