Interested in Maxwell?
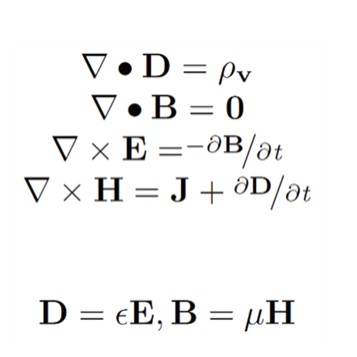

James Clerk Maxwell
Scottish born math genius. Middle name pronounced "Clark." Unified the experimental work of Volta, Ampere and others by describing the phenomenas of electricity and magnetism as a single natural force electromagnetism.
Maxwell used his superior math skills to mathematically describe how electricity and magnetism interact. Little known is that Maxwell actually used 10 equations to describe electromagnetism. Oliver Heaviside removed the non-intuitive concept of magnetic moment and was thereby able to simplify the original equations to 4, which are now commonly called "Maxwell's equations"
Let's get after those equations!!
Equation 1 reads "Divergence of D(electric flux density) equals average enclosed charge per volume."
Easy! That's just electrostatics. Divergence is how many flux lines originate in an enclosed volume. More average charge = more flux lines. Can be positive (source) or negative (sink.) If no source or sink, then divergence is 0.
Equation 2 reads "Divergence of B(magnetic flux density) is equal to zero."
My favorite equation!! Magnetostatics in this case. This equation means that you can never cut a magnet in half. You can try, but you'll just end up with 2 magnets. No magnetic unipoles is what this equation tells us. This also means sources and sinks must exist in unison.
Equation 3 reads "Curl of E (electric field intensity) equals negative partial derivative of B (magnetic flux density) over partial derivative of time.
Notice the presence of time in this equation. This means we are in a time-varying or dynamic system. Also, notice both electric and magnetic terms. This is electromagnetism and is one of the 4 fundamental forces of nature (the others are gravity and the strong and weak nuclear forces.) Curl is from vector calculus and uses a cross product. This means forces are in three different directions. You can think of this like a screwdriver. You twist, which is a two direction mechanical couple, and the drives down in the third direction. The curl of E is how much electric potential is induced when encountering changing magnetic flux lines. This equation explains why a spinning permanent magnet can induce a current in a wire
Equation 4 reads curl of H (magnetic field intensity) equals J (drift current) plus partial derivative of D (electric flux density) over partial derivative of time.
More dynamics. This time explaining the magnetic fields induced by moving eletric charge. A steady current will induced a steady magnetic field and a dynamic current will induce a dynamic magnetic field. This dynamic magnetic field is electromagnetic waves and explain how and antenna can be used to broadcast and receive radio waves.
The final two equations relate field intensity to flux density based on epsilon and mu, which are constants based on material and can either dampen or amplify flux density. This explains why capacitor dielectrics are so important, and also why electromagnets are wrapped around permanent magnets.
Notice that both tables start about 1 which is free space. Permittivity starts exactly at 1 and then increases only to ~80. However, permeability values can decrease slightly below free space. Also, the max value is around 5000! Another fun fact is that non-magnetic materials all have values around 1, but slightly different from each other and can be both above and below 1. An MRI exploits this fact. Since the body is entirely non-magnetic, strong magnetic fields will have minimal effects on the body. Each different tissue charges up its resonant frequency dictated by its relative permittivity, and then can be measured by how long the field takes to return to normal. Magnetic Resonance Imaging. Get it?
Statics
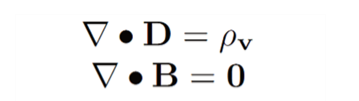
Dynamics
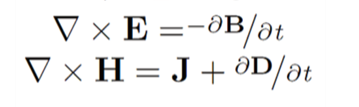
Intensity vs. density
Heinrich Hertz
Master experimenter
Mr. Hertz was inspired by Maxwell's prediction of electromagnetic waves and proved their existence. In his honor, the fundamental unit of frequency was named after him.
Hertz doubted his discovery would have any practical uses, and died early so was not able to see how thoroughly electromagnetics has changed the world.
We need your consent to load the translations
We use a third-party service to translate the website content that may collect data about your activity. Please review the details in the privacy policy and accept the service to view the translations.